Killing the hydra
In this post, we discuss the Kirby–Paris Hydra game, which involves killing off a particularly vicious modern variant of the Lernaean Hydra. This post is essentially a less technical rewrite of the paper “Accessible Independence Results for Peano Arithmetic” by Laurie Kirby and Jeff Paris.
1. The Hydra Game
Let us begin with a tale from Greek mythology.
In the first version, Hercules, the bastard son of Zeus, is driven mad by the jealous goddess of marriage and kills his own children. The Oracle at Delphi advised Hercules to wash away his sins by serving King Eurystheus, who was under Hera’s sway. Hercules is then ordered to carry out ten grueling tasks, and then two more for accepting assistance. These tasks are known as the Twelve Labors of Hercules.
One of the two nullified Labors was to kill the Lernaean Hydra, a many-headed monster who grew two heads each time one of its heads was cut off. By having his cousin burn off the Hydra’s neck after each decapitation, Hercules was able to stop the vicious cycle and prevail. Since Hercules could not have done this on his own, Hera disapproved, and so did King Eurystheus.
It is only fair to give Hercules another chance. After all, the judge of the match was biased—extremely so, as she was the one who started the whole trouble.
We thus offer the second version, in which Hercules fights the Hydra on his own. Unfortunately, the Hydras have evolved over time, and the modern-day Hydra that Hercules faces today grows many heads instead of two.
To be precise, we think of the Hydra as a graph, a mathematical object composed of nodes and segments that connect them. We stipulate further that the Hydra has only one body, i.e., every node is connected by a unique path of segments to a fixed node called the root.
A modern-day Hydra might therefore look like this:
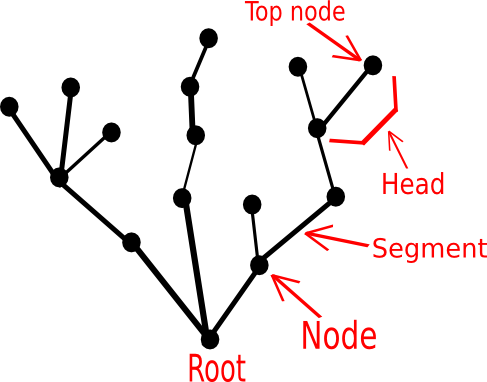
Figure 1. A modern-day Hydra, represented as a graph
A top node is defined to be a node that is connected to only one edge. Placing the root at the bottom and drawing the Hydra upwards, we see that the “top nodes” are indeed at the top. We then define a head to be the combination of a top node with the unique edge connected to it.
Since we are dealing with a Hydra, after all, we should expect it to regenerate every time we decapitate it. The following rules apply for each round of head-chopping, rendering our modern-day Hydra much more vicious than its classical counterpart:
- Hercules severs a head. In the diagram below, he cuts off the head labelled in red.
- Go to the node right below the node connected to the severed head—labelled in purple in the diagram—and reproduce n copies of all the nodes and the segments above the selected node. Here, n is the number of times Hercules has attacked the Hydra thus far. For example, if we assume that the head labelled in red is the third head that Hercules has cut off so far, then the part labelled in blue should be copied 3 times, resulting in 4 copies of it in total.
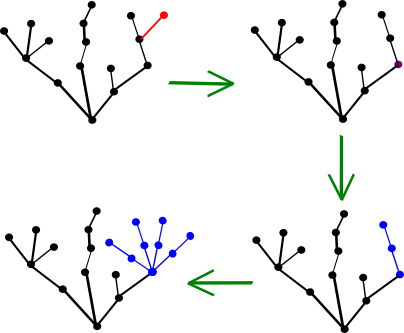
Figure 2. Decapitation; regeneration
A natural question to ask at this stage is the following:
Question 1. Is there a winning strategy? In other words, is there a finite sequence of moves that Hercules could perform on the Hydra that will remove all but the root of the Hydra? (You could try playing the Hydra game yourself!)
At the outset, the task of killing the new Hydra appears hopeless. Will there be a happy ending to the story of our modern-day Hercules?
2. Goodstein Sequences
In order to amass the necessary mathematical machinery to tackle Question 1, let us take a detour and consider a sequence of numbers that grows very fast, just like the number of the heads of the Hydra. The Goodstein sequence of a natural number $n$ is generated as follows:
- Set the first term $ g_1 $ to be $ n $. For concreteness, let us take $ n = 5 $, so that $ g_1 = 5 $.
- Write $ g_1 $ in hereditary base 2. This means that we can only use additions, multiplications, and exponentiations of the numbers 2, 1, and 0. For example, we can write $ g_1 = 5 = 2^2 + 1 $ .
- Take the hereditary base 2 expansion of $g_1 $ obtained above change all the 2s to 3s, and subtract 1. The resulting number is $g_2$. In our case, we transform $2^2 + 1$ to $3^3 + 1$, and then remove 1 to obtain $3^3$, which we set as $g_2$.
- Write $ g_2 $ in hereditary base 3—similarly as in 2, but now allowing the numbers 3, 2, 1, and 0. For example, $g_2 = 3^3 + 3$ is already in hereditary base 3.
- Take the hereditary base 3 expansion of $ g_2 $ obtained above, change all the 3s to 4s, and subtract 1. The resulting number is $g_3$ . In our case, we transform $3^3$ to $4^4$ and then remove 1 to obtain $4^4 - 1$, which we set to be $g_3$.
- Write $ g_3 $ in hereditary base 4. In our case, this step more work than usual, since we cannot leave the $-1$ at the end. We remedy the situation by rewriting $4^4-1$ as follows: $$\begin{align*} 4^4 - 1 &= (4-1)(4^3 + 4^2 + 4 + 1) \\ &= 3 \cdot 4^3 + 3 \cdot 4^2 \\ &+ 3 \cdot 4 + 3. \end{align*}$$ Here we have used the standard factoring trick $$x^n - 1 = (x-1)(x^{n-1} + x^{n-2} + \cdots + x + 1).$$
- Repeat the above process to obtain $g_4$, $g_5$, and so on.
Evidently, the Goodstein sequences grow quite fast. Here is a table of the first few terms of the Goodstein sequence of 19:
$$\begin{align*} g_1 & = 19 = 1.9 \cdot 10^1 \\ g_2 & = 7625597484990 \approx 7.6 \cdot 10^{12} \\ g_3 & \approx 1.3 \cdot 10^{154} \\ g_4 & \approx 1.8 \cdot 10^{2184} \\ g_5 & \approx 2.6 \cdot 10^{36305} \end{align*}$$
This is just like the task of killing the Hydra: to think that this sequence will ever decrease would appear to be downright foolish. Nevertheless, the following is true:
Theorem 2 (Goodstein). The Goodstein sequence of any natural number terminates to zero. In other words, given any Goodstein sequence $(g_n)_{n=1}^\infty$, there exists a natural number $N$ such that $n \geq N$ implies $g_n = 0$.
How could this be?
3. Ordinal Numbers and the Well-Ordering Principle
To prove Goodstein’s theorem, we recall a simple but fundamental fact about the usual ordering of numbers:
Proposition 3 (Trichotomy principle). One, and only one, of the following must hold for each pair of numbers \(x\) and \(y\):
- \(x < y\);
- \(x = y\);
- \(x > y\).
Therefore, if $ x \leq y \leq x $, then the trichotomy principle forces us to conclude that $ x = y $. In particular, if a nonnegative number is bounded above by 0, then it must be 0 itself as well.
Since each term of the Goodstein sequence is nonnegative, we would be able to prove Goodstein’s theorem by producing a sequence of numbers decreasing to zero that bounds the Goodstein sequence from above. This might seem even more unreasonable than trying to prove Goodstein’s theorem directly. Showing that the Goodstein sequence decreases to 0 looks hard enough. How are we supposed to find an even larger sequence that goes to 0? The key is the following property of natural numbers:
Proposition 4 (Well-ordering principle for natural numbers). If \( (x_{n})_{n=1}^\infty \) is a sequence of natural numbers that is *strictly decreasing*, viz., \( x_{n} > x_{n+1} \) for each index \(n\), then \((x_{n})_{n=1}^\infty\) terminates to zero.
In other words, it suffices to find a sequence of upper bounds that is strictly decreasing. The well-ordering principle, in tandem with the trichotomy principle, will then guarantee the termination of the sequence in question.
It is important to note that the well-ordering principle does not necessarily hold for other number systems. The sequence of integers
$$5,4,3,2,1,0,-1,-2,-3,\ldots$$
evidently does not terminate to zero, whence the integers do not satisfy the well-ordering principle. On the other hand, it is not hard to see that a strictly decreasing sequence of natural numbers whose first term is $ n $ will terminate to zero in $ n $ steps or fewer.
Admittedly, it is still not very clear how we would go about creating a strictly decreasing sequence that bounds the Goodstein sequence from above. Surely, we would need a sequence of very large numbers to do this. In fact, wouldn’t a sequence of “decreasing infinities” (whatever that means) do the job? “Infinities” would of course be larger than any natural number, and then we might hope to be able to generalize the well-ordering principle to these “infinities” to conclude that the “decreasing sequence of infinities” terminates to zero.
To make this idea rigorous, we introduce the ordinal numbers as follows:
- Enumerate the natural numbers: 0, 1, 2, 3, 4, …
- Declare $ \omega $ to be the number that comes after all the natural numbers. The first infinite ordinal, if you will.
- Enumerate the numbers that comes after $ \omega $: $ \omega+1,\omega+2,\omega+3,\ldots $ .
- Declare $ 2\omega $ to be the number that comes after all the numbers in Step 3.
- Similarly as in Step 3, count the numbers that comes after $ 2\omega $: $ 2\omega+1,2\omega+2,2\omega+3,\ldots $ .
- Similarly as in Step 4, we introduce $ 2\omega,3\omega,4\omega,\ldots $ . We also introduce the numbers that come after each of those omegas, as we did in Steps 3 and 5.
- Declare $ \omega^2 $ to be the number that comes after all the numbers in Step 6. We can now introduce $ 2\omega^2,3\omega^2,4\omega^2,\ldots $ and all the numbers in between.
- Similarly as in Step 7, we introduce $ \omega^3,\omega^4,\omega^5,\ldots $ and all the numbers in between.
- Declare $ \omega^\omega $ to be the number that comes after all the numbers in Step 8. We can now introduce $ \omega^{\omega^2},\omega^{\omega^3},\omega^{\omega^4},\ldots $ and all the numbers in between.
- Similarly as in Step 9, we introduce $$ \omega^{\omega^\omega},\omega^{\omega^{\omega^\omega}},\omega^{\omega^{\omega^{\omega^\omega}}},\ldots $$ and all the numbers in between.
We could continue, but these are all we will need for the proof of Goodstein’s theorem. The way we constructed these new “infinite numbers” implies the following ordering:
$$\begin{array}{c} 1 < 2 < \cdots < n < n+1 < \cdots < \omega < \omega+1 < \cdots \\ < \omega + n < \omega + n + 1 < \cdots < 2 \omega < \cdots < n \omega < \cdots \\ < \omega^2 < \cdots < \omega^3 < \cdots < \omega^\omega < \cdots < \omega^{\omega^\omega} < \cdots. \end{array}$$
Moreover, the ordinals retain the well-ordering property.
A strictly decreasing sequence of ordinals whose first term is, let’s say, $ 3\omega^\omega+4 $, falls below $ 3 \omega^\omega $ after 4 steps or less. It then falls below $ 2 \omega^\omega $ after finitely many steps, and then below $ \omega^\omega $.
But “falling below $ \omega^\omega $ means that the remaining terms of the sequence are now smaller than $ n\omega^m $ for some $ n $ and $ m $. Therefore, the sequence falls below $ n \omega^{m-1} $, and then below $ n \omega^{m-2} $, all the way down below $ n \omega $.
Reasoning analogously, we see that the remaining terms of the sequence will eventually be smaller than $\omega $, at which point we apply the well-ordering principle for natural numbers (Proposition 4) to conclude that the remaining terms will terminate to zero.
Since each step was finitary, the terminating process takes finitely many steps. The above argument can be repeated verbatim for any strictly decreasing sequence of ordinals. We have thus proved the following lemma:
Lemma 5 (Well-ordering principle for ordinals). If $(x_{n})^\infty_{n=1}$ is a strictly decreasing sequence of ordinal numbers, then $(x_{n})^\infty_{n=1}$ terminates to zero.
4. Proof of Goodstein’s Theorem
With ordinal numbers in our arsenal, let us now return to Goodstein’s theorem. We produce the strictly decreasing sequence of upper bounds ((x_{n})_{n=1}^\infty) as follows:
- Obtain $ x_1 $ by changing all the 2’s in $ g_1 $ to $ \omega $. For example, if $ g_1 = 5 = 2^2 + 1 $, then $ x_1 = \omega^\omega + 1 $.
- Obtain $ x_2 $ by changing all the 3’s in $ g_2 $ to $ \omega $. In our case, we have $ g_2 = 3^3 $, and so $ x_2 = \omega^\omega $.
- Obtain $ x_3 $ by changing all the 4’s in $ g_3 $ to $ \omega $. In our case, we have $ g_3 = 3 \cdot 4^3 + 3 \cdot 4^2 + 3 \cdot 4 + 3 $, and so $ x_3 = 3\omega^3 + 3 \omega^2 + 3\omega+3 $.
- Continue analogously to obtain $ x_4,x_5,x_6,\ldots $.
Since we are replacing finite numbers with infinite numbers, $ x_n $ evidently serves as an upper bound for $ g_n $. Note, however, that the “subtract 1” operation at each step of the construction of Goodstein’s sequence causes the sequence of upper bounds to decrease strictly. In fact, $(x_n)^\infty_{n=1}$ decreases significantly whenever we have to rewrite the Goodstein term via the factoring trick (see Step 6 in the construction of the Goodstein sequence). It now follows from the well-ordering principle for ordinals (Lemma 5) that the sequence of upper bounds $(x_n)^\infty_{n=1}$ terminates to zero, whence the trichotomy principle (Proposition 3) implies that the Goodstein sequence in question must terminate to zero as well. This completes the proof of Goodstein’s theorem.
5. Solution to the Hydra Game
And so we have successfully terminated the monstrous Goodstein sequence to zero. In this manner, we shall terminate the modern-day Hydra as well. To relate the hydra game to the proof of Goodstein’s theorem, we define the complexity of the Hydra at each step as an ordinal representing how “large” the Hydra is, so that the Hydra of complexity zero corresponds to the Hydra with all of its heads chopped off. Specifically, we define complexity as follows:
- Label each top node 0.
- Go down a node. The label for this node is the sum of the number of the top nodes connected to it.
- Go down a node. If there is only one node above it, then the label for this node is $ \omega^L $, where $ L $ is the label for the node above this node. If there are multiple nodes above this node, with labels $ L_1,\ldots,L_n $, then the label for the node in question is given by $ \omega^{L_1}+\cdots+\omega^{L_n} $.
- Continue the process until the root is reached. The label for the root is the complexity for the Hydra.
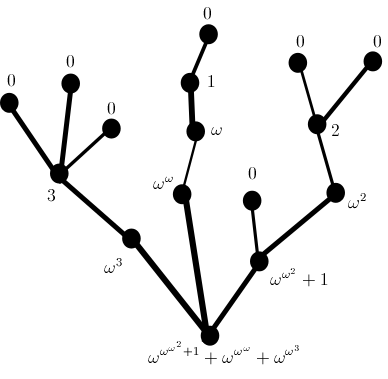
Figure 3. Complexity diagram of the Hydra
The point is that the contribution of a head to the overall complexity to the Hydra is proportional to its distance to the root. Therefore, the act of chopping of a head reduces the complexity of the Hydra, as the regenerated heads are closer to the root than the head that was cut off. It does not matter if decapitation results in a higher number of heads—even if the Hydra grew 999 new heads, $ \omega^{999} $ would still be lot smaller than $ \omega^\omega $ . We thus end up with a strictly decreasing sequence of complexities, whence we conclude that the complexity sequence must terminate to zero. This means that we can always kill the Hydra: in other words, every strategy is a winning strategy.
6. Further Results: Set-Theoretic Independence
You might think it strange that we resorted to an “appeal to infinity” argument in order to prove a statement about the natural numbers, which are finitary objects. You might protest, there must be a way to solve the Hydra game without this black magic! And of course, the world shouldn’t be this strange! But, sadly, we cannot prove Goodstein’s theorem or the solution to the Hydra game without utilizing some sort of infinitary argument. In fact, Kirby and Paris proved that the language of natural numbers is insufficient to establish Goodstein’s theorem. To put this in fancy terms: Goodstein’s theorem is independent of the axioms of the natural numbers.
What does that last statement mean? A mathematical theory is a collection of mathematical statements that can be deduced from axioms, which are mathematical statements we assume to be valid a priori. You might remember the postulates of Euclidean geometry from high school:
- Given two points, we can always draw a straight line between them.
- Given a straight line, we can always extend it in either direction.
- Given a point $ x $ and a positive number $ r $, we can always draw a circle of radius $ r $ centered at $ x $.
- All right angles are congruent.
- Given a line $ L $ and a point $ x $ not on $ L $, we can draw at most one line parallel to $ L $ that goes through $ x $.
In this case, the postulates are the axioms, and Euclidean geometry is the mathematical theory derived from the axioms. You might also remember the fuss about the last postulate, which is commonly known as the parallel postulate. Your geometry teacher might even have challenged your class to derive the parallel postulate from the other four axioms—with a prize, even. This is a common yet devious trick amongst math teachers, as the parallel postulate is known to be unprovable from the first four postulates of Euclidean geometry.
To see why, let us recall one of the most fundamental results of Euclidean geometry: the sum of the angles of a triangle is 180º. The usual textbook proof of this makes use of the parallel postulate but does not demonstrate that the parallel postulate is necessary. If we could derive the parallel postulate from the first four axioms, then surely we could deduce the angle-sum result from the first four as well. Therefore, establishing the necessity boils down to developing alternate theories of geometry, deducible from the first four postulates, in which the sum of the angles of a triangle is not necessarily 180º. And the geometers of the 19th century did just that:

Figure 4. Elliptic geometry (source: Wikipedia)
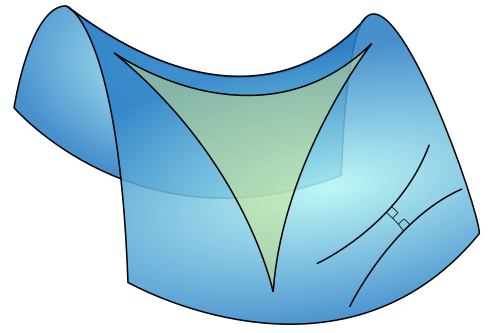
Figure 5. Hyperbolic geometry (source: Wikipedia)
It follows that the parallel postulate cannot be deduced from the first four postulates. In the language of mathematical logic, we say that the parallel postulate is independent of the first four postulates.
What about Goodstein’s theorem? The theory of natural numbers is governed by Peano’s axioms, which is a collection of statements about fundamental properties of natural numbers. Similarly as the above examples of non-Euclidean geometry, Kirby and Paris created another theory of natural numbers in which Goodstein’s theorem fails, thereby showing that Goodstein’s theorem lies outside of the scope of Peano’s axioms. Goodstein’s theorem is independent of Peano’s axioms, and Peano’s axioms are not strong enough to either prove or disprove Goodstein’s theorem.
The implication is that there might be yes-or-no questions that we could answer neither affirmatively nor negatively, at least within the given theory. It could be that the mathematical theory at hand was simply not comprehensive enough: after all, appending the theory of ordinal numbers to Peano’s axioms was enough to prove Goodstein’s theorem. Perhaps we could come up with a comprehensive enough theory that could determine the validity of each and every statement.
Not so, unfortunately. The famed Gödel incompleteness theorem states that every consistent axiomatic system comprehensive enough to subsume the theory of natural numbers admits statements that are independent to the system; here consistent means that the theory never says something is both true and false at the same time, which is evidently a desirable property. No matter how hard we try to strengthen the theory at hand, there will always be mathematical questions that our theory will not be strong enough to answer.
If you want to know more about the Gödel incompleteness theorem, a celebrated account of the theory geared towards the general public can be found in the book of Nagel and Newman. Another natural question is whether we could determine a given statement is independent of a standard mathematical theory. The study of independence issues often involves a technical tool from set theory known as forcing, developed by Paul Cohen to settle the Continuum hypothesis, which is one of the most famous mathematical problems of the twentieth century. A less technical (but technical nevertheless) account of the technique of forcing can be found in the article of Timothy Chow. Understanding forcing requires a working knowledge of set theory at the college level, much of which can be gleaned from the beautifully written textbook by Paul Halmos. Modern textbooks such as Jech and Hrbacek provide more comprehensive treatments and are better suited for in-depth studies.